树堆的基本概念
树堆(Treap)是二叉排序树(Binary Sort Tree)与堆(Heap)结合产生的一种拥有堆性质的二叉排序树。
但是这里要注意两点,第一点是Treap和二叉堆有一点不同,就是二叉堆必须是完全二叉树,而Treap并不一定是;第二点是Treap并不严格满足平衡二叉排序树(AVL树)的要求,即树堆中每个节点的左右子树高度之差的绝对值可能会超过1,只是近似满足平衡二叉排序树的性质。
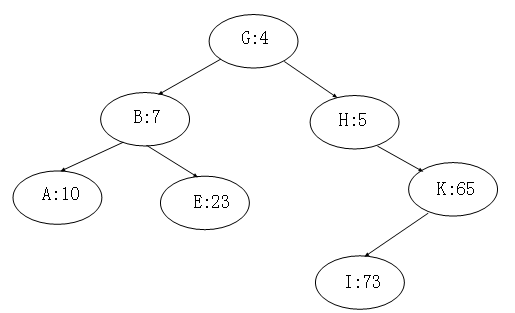
Treap每个节点记录两个数据,一个是键值,一个是随机附加的优先级,Treap在以关键码构成二叉排序树的同时,又以结点优先级形成最大堆和最小堆。所以Treap必须满足这两个性质,一是二叉排序树的性质,二是堆的性质。如下图,即为一个树堆。
关键步骤
查找
按照正常BST的查找过程即可
插入
- 给新节点一个随机的权重值,按照普通二叉搜索树,使用key进行插入
- 为了保证堆的特性,插入完成后要进行旋转操作,保证仍为最大堆或最小堆。以最大堆为例,若插入到右子树,且权重比父结点大,就要实现一次左旋转,使右子树根结点成为新的父节点;反之左旋,直到满足堆的特性为止
删除
- 按照正常的查找流程找到待删除节点后,有三种情况
- 待删除结点本身就是叶子结点,直接删除即可
- 待删除结点只有一个孩子(一棵子树),用这个孩子替换待删除结点,实现删除效果
- 待删除结点两棵子树均不为空时,先进行旋转。以最大堆为例,找到权重更大的孩子,向相反方向旋转(即若左孩子权重更大,执行右旋),直到待删除结点满足上面两种情况之一,再进行删除
具体实现
参考LeetCode(cn) 第1438题的实现,其中对于旋转的优雅实现值得一学
import "math/rand"
type node struct {
ch [2]*node
priority int
key int
cnt int
}
func (o *node) cmp(b int) int {
switch {
case b < o.key:
return 0
case b > o.key:
return 1
default:
return -1
}
}
func (o *node) rotate(d int) *node {
x := o.ch[d^1]
o.ch[d^1] = x.ch[d]
x.ch[d] = o
return x
}
type treap struct {
root *node
}
func (t *treap) ins(o *node, key int) *node {
if o == nil {
return &node{priority: rand.Int(), key: key, cnt: 1}
}
if d := o.cmp(key); d >= 0 {
o.ch[d] = t.ins(o.ch[d], key)
if o.ch[d].priority > o.priority {
o = o.rotate(d ^ 1)
}
} else {
o.cnt++
}
return o
}
func (t *treap) del(o *node, key int) *node {
if o == nil {
return nil
}
if d := o.cmp(key); d >= 0 {
o.ch[d] = t.del(o.ch[d], key)
} else {
if o.cnt > 1 {
o.cnt--
} else {
if o.ch[1] == nil {
return o.ch[0]
}
if o.ch[0] == nil {
return o.ch[1]
}
d = 0
if o.ch[0].priority > o.ch[1].priority {
d = 1
}
o = o.rotate(d)
o.ch[d] = t.del(o.ch[d], key)
}
}
return o
}
func (t *treap) insert(key int) {
t.root = t.ins(t.root, key)
}
func (t *treap) delete(key int) {
t.root = t.del(t.root, key)
}
func (t *treap) min() (min *node) {
for o := t.root; o != nil; o = o.ch[0] {
min = o
}
return
}
func (t *treap) max() (max *node) {
for o := t.root; o != nil; o = o.ch[1] {
max = o
}
return
}
func longestSubarray(nums []int, limit int) (ans int) {
t := &treap{}
left := 0
for right, v := range nums {
t.insert(v)
for t.max().key-t.min().key > limit {
t.delete(nums[left])
left++
}
ans = max(ans, right-left+1)
}
return
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
参考
树堆(Treap)图文详解与实现
leecode-cn 1438