smp cdn

稳定婚姻问题及其在CDN调度分发中的应用

Posted by ChaosNyaruko on April 16, 2021

稳定婚姻问题

Stable Marriage Problem定义

两个集合men、women数量相等，每个人持有对异性的好感度顺序表。现在假定要对这n对进行匹配，如果某种匹配存在同时满足以下三个条件的m-w对(blocking-pair)，则认为此匹配是不稳定的：1)m和w目前没有订婚（意味着它们的订婚对象是别人） 2) 在m的优先级列表中，w的级别比当前订婚对象高 3) 在w的优先级列表中，m的优先级比当前订婚对象优先级高。 反之则称这个匹配是稳定的。在这样一个场景中求解稳定订婚关系的问题，称之为稳定婚姻问题

常见变种

  • SMI:(SM with Incomplete lists)

  • SMT:(SM with Ties)

    按照稳定条件依次减弱

    • super-stability

    • strong stability

    • weak stability: 总是存在解，并能在多项式时间内解决

  • SMTI(SM with Ties and Incomplete lists)

    • 三种稳定关系定义，同上

    • super/strong关系，存在算法可以确定一个问题是否有解，以及求出一个解，super stability时间复杂度O(a), strong stabilityO(na)， a表示所有优先级列表的整体长度（2n^2如果所有优先级列表都是完整的），且所有的解都具有相同的大小

    • weak stablity，任何情况下都存在一个稳定匹配，并且可以在O(a)时间内找到，但是解的大小可以有多个，求解其中最大的那个是NP-Hard的

经典解法

Gale-Shapley Algorithm

algorithm stable_matching is

    Initialize all m ∈ M and w ∈ W to free

    while ∃ free man m who still has a woman w to propose to do

        w := first woman on m's list to whom m has not yet proposed

        if w is free then

            (m, w) become engaged

        else some pair (m', w) already exists

            if w prefers m to m' then

                m' becomes free

                (m, w) become engaged 

            else

                (m', w) remain engaged

            end if

        end if

    repeat

  • 按轮次进行

  • 每一轮求婚过程都由尚未订婚的男方m发起，对自己尚未求过婚的女性中选择优先级最高的w，若该女性目前也是单身，则(m,w)订婚关系暂时成立；否则假设当时与w的订婚对象是m’：
    • 若w更中意m，那么w与m’的关系取消，转而与m订婚，与此同时，m’成为单身（意味着他可以在下一轮进行选择）

  • 否则(m’,w)关系保持，m之后需要尝试向次优选择求婚

  • 直到所有的男性没有可求婚对象（即都有订婚关系以后）循环结束，问题得解

img

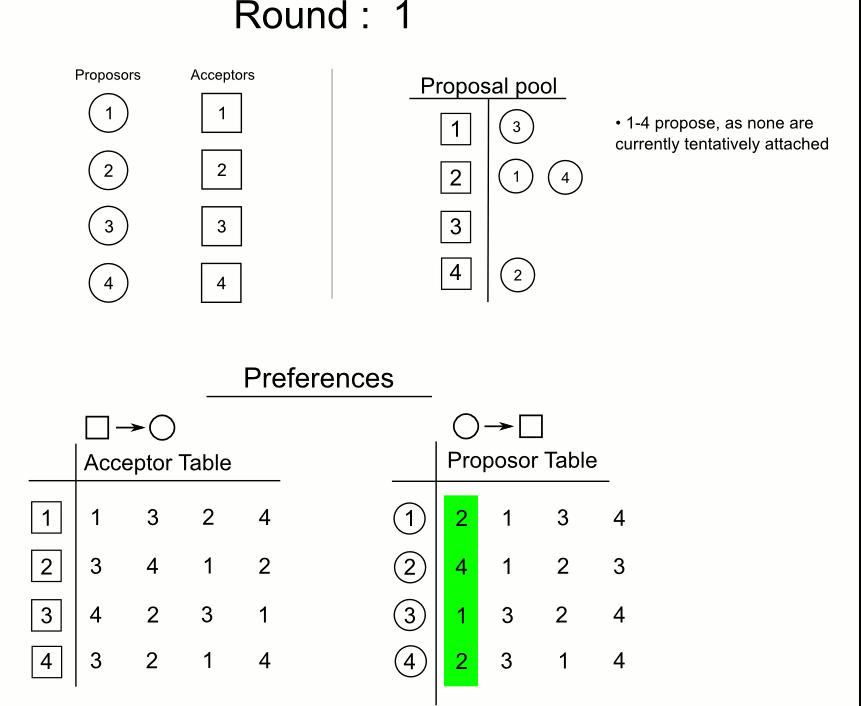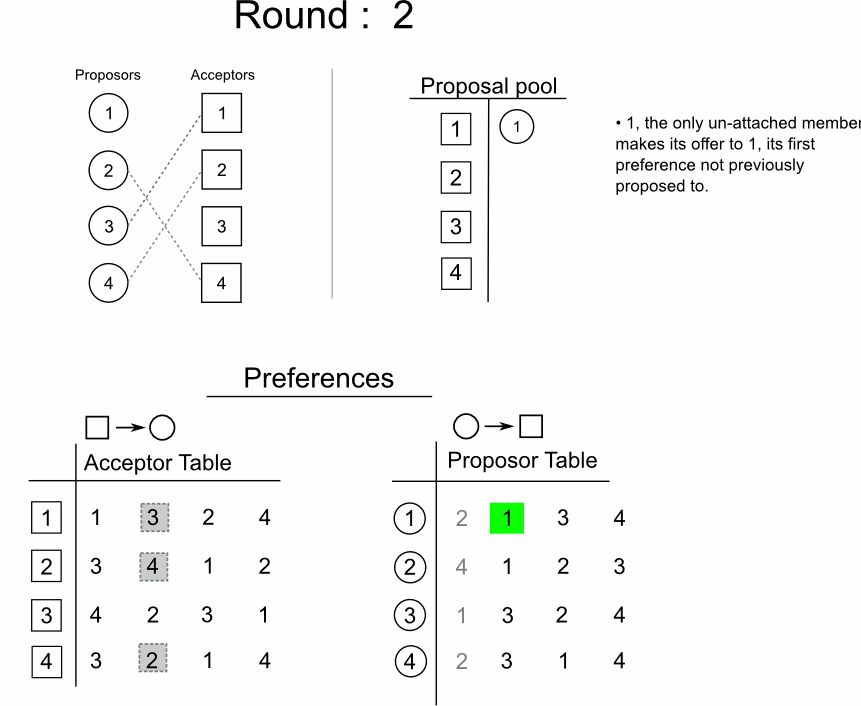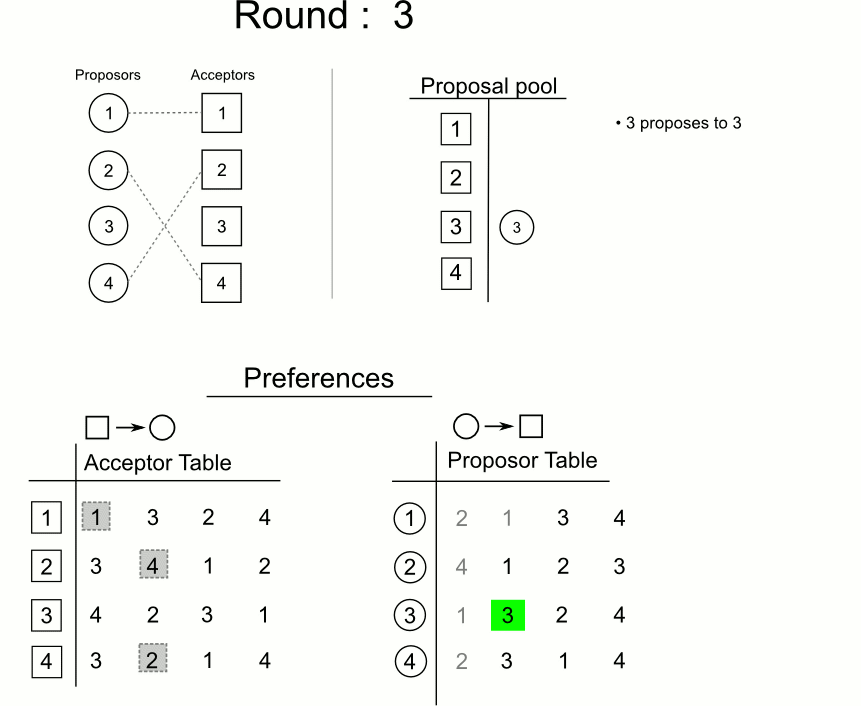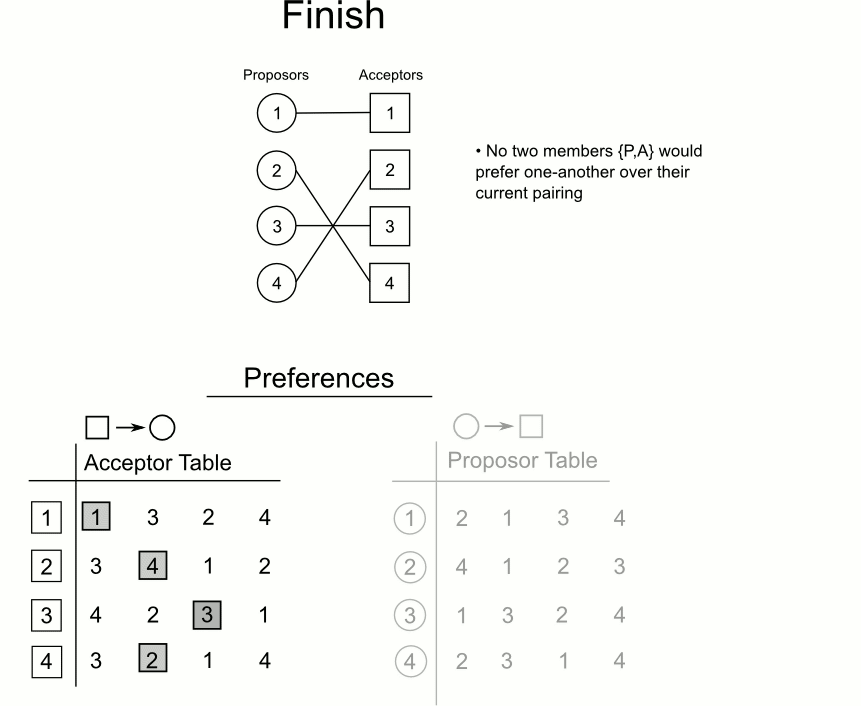
分步：

img

img

img

img

img

img

img

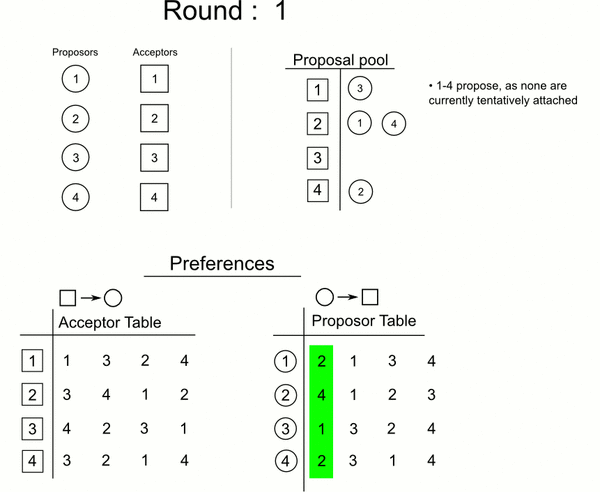
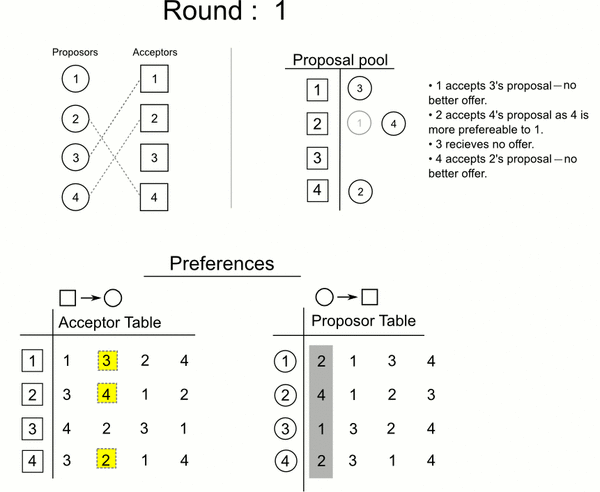
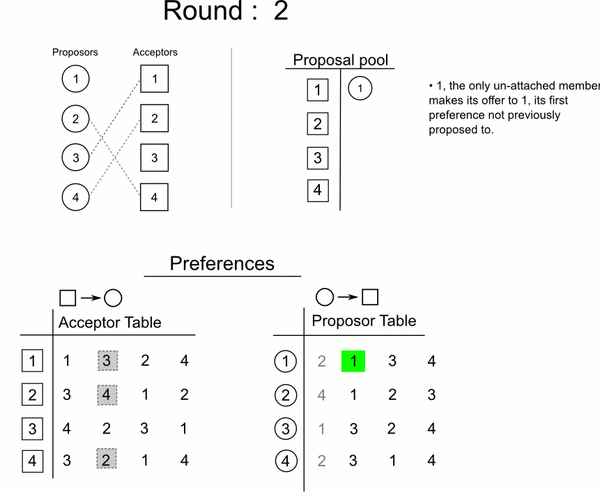
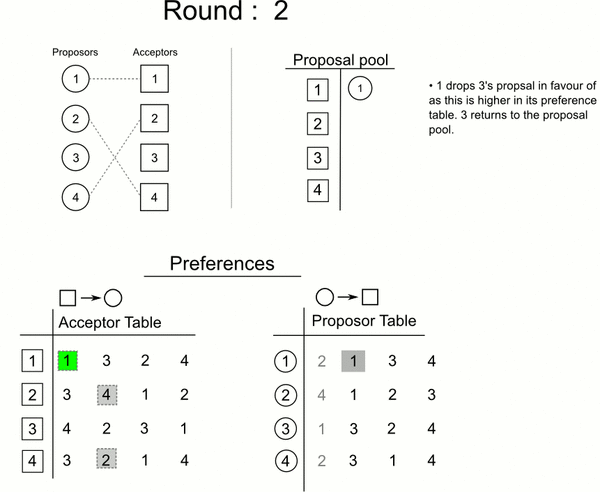
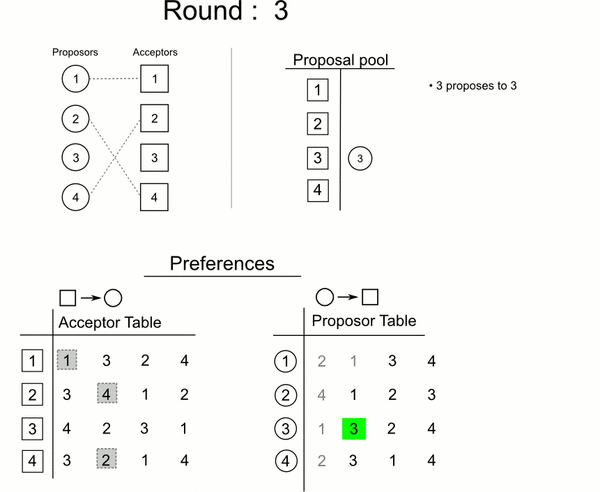
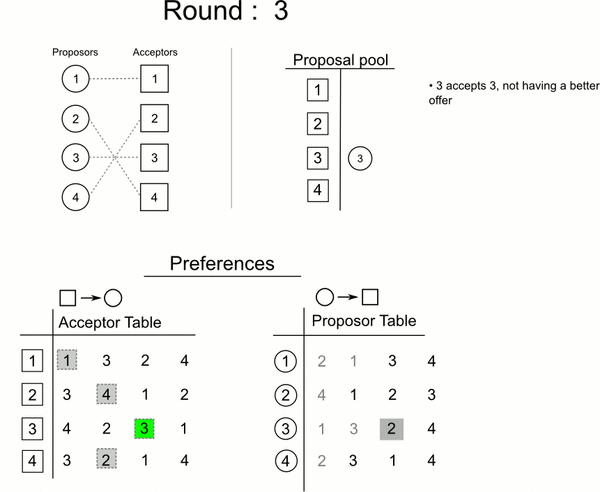
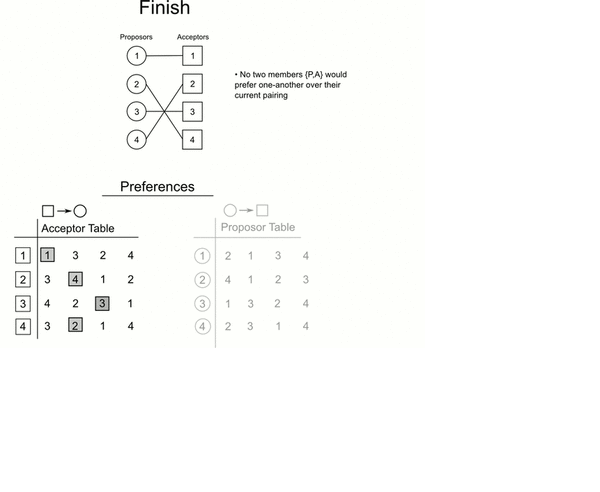
  • 时间复杂度O(n^2)

  • 保证算法最后所有人都有订婚对象

  • 最后形成的关系是稳定的

  • man-optimal/woman-pessimal

在全局负载均衡网络中的应用

负载均衡就是要把对应客户端的请求打到最合适的CDN服务器节点/集群上（映射）

模型抽象

map unit

tuple: <IP address prefix, traffic class>

如<1.2.3.4/24, video> <1.2.3.4/24, web>

Mi, Cj, di cj

img

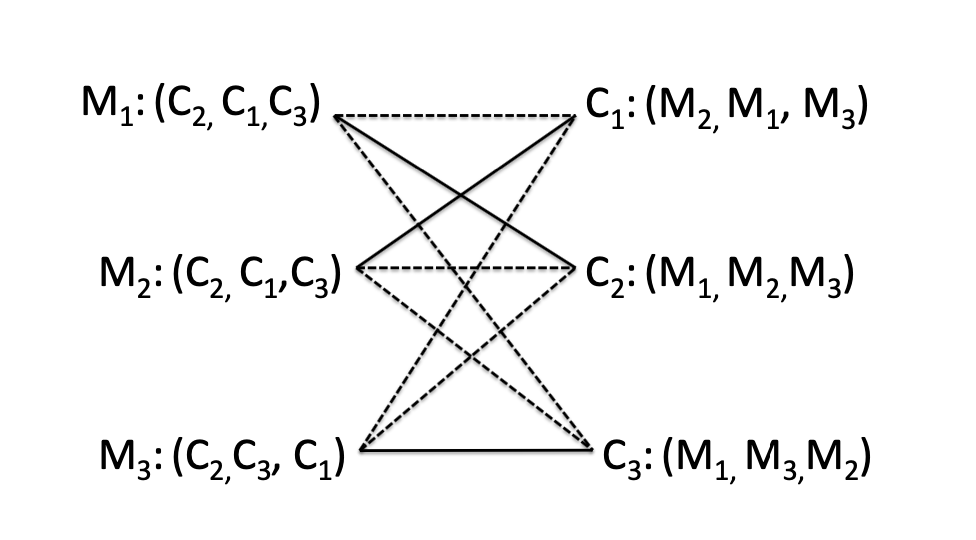
变种特性

  • map units和clusters的数量不同

  • 优先级列表不完全

  • demands 和 capacities的资源化

Resource Trees

  • 服务器并不单独服务于某种单一服务

  • 不同类型的业务消耗的资源类型重点不一样

img

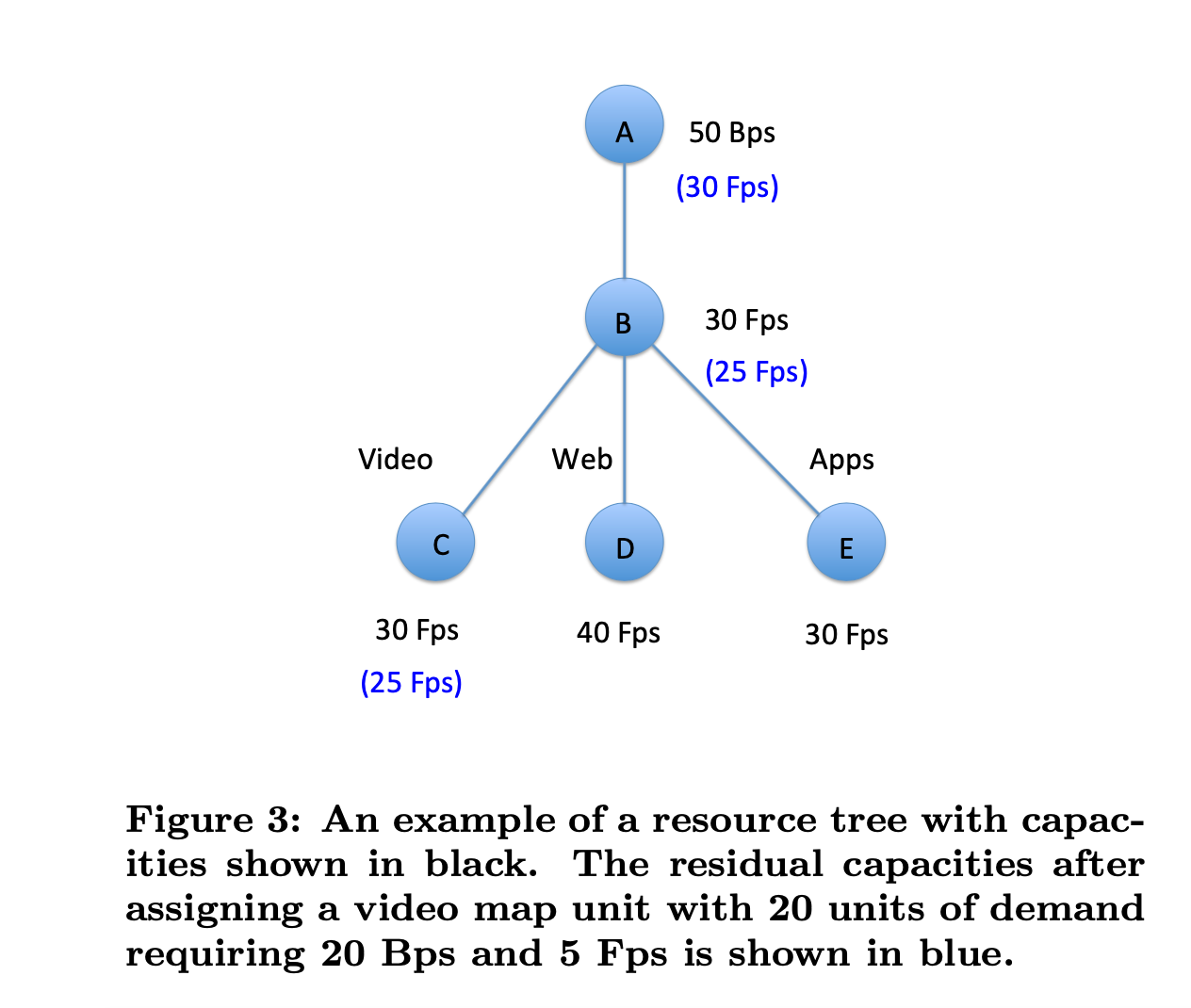
Bps: bytes per second

Fps: “flytes” per second

叶子节点标识每种traffic class可用的最大Fps资源，父亲节点B标识这个集群上所有traffic共用下Fps的最大可用资源，根节点A表示可从该集群发送的最大Bps资源

这棵树展现了一种评估服务资源约束的方法。一个map unit从叶子节点开始向上计算，直到根节点也满足资源约束时才是满足需求的。

举个例子：一个访问video的demand本身要f Fps和b Bps(f,b是每个demand的比例系数)。一个map unit发出20个单位的video demand,f=0.25, b=1，那么总共需要5个Fps和20个Bps

G-S算法有对应的适配[13]

f=1 b=0.25，demand=26 —> 26 Fps 和 6.5Bps，在节点B不满足约束，但是A和E满足。假设集群有个优先级列表，优先服务Apps，那么4个单位的video demand就会被逐出，从而在节点B创造出额外的1 Fps，使这26个app demand能被顺利处理

类似上述过程不断重分配，以收敛到稳定分配的状态

实际挑战

  • 复杂度和问题规模

    数量级极大的map units, clusters以及更复杂的resource trees

  • 计算时间

    对于map unit的分配10~30秒就要计算一次，G-S算法的时间复杂度足够优秀，并且可以改造成分布式的以进行并行计算

  • demand和capacity的估算

    对于资源模型的抽象也是一个难点，一方面，它们是可以不断变化的，另一方面，之前所提的比例系数在实际应用当中也是相当难以估计，经常是需要当demand被实际分配给了一个cluster之后，才能确定。所以，可能需要一个完善的反馈/闭环，以便基于历史尽可能准确地估计demand和capacity

  • 增量分配和持久性

    之前所述的解决方法是基于完整的分配问题，也就是说每次从头开始计算，这在实际应用中其实是并不太理想的。[2]中阐述了两个原因：一是一般情况下只有一小部分的map unit需要重分配（就是那些优先度列表发生较大变化的）；二是对整个分配的重计算可能导致分配关系的大幅变动，即便元数据变化不大， 这样会导致CDN的命中率下降. (needs a “sticky” solution)，不然的话甚至可能引起震荡。

参考

[1] Kazuo Iwama and Shuichi Miyazaki. A survey of the stable marriage problem and its variants. In Informatics Education and Research for Knowledge-Circulating Society, 2008. ICKS 2008. https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/226940/1/ICKS.2008.7.pdf

[2] Algorithmic Nuggets in Content Delivery

[3] https://en.wikipedia.org/wiki/Stable_marriage_problem

[4] https://en.wikipedia.org/wiki/Gale%E2%80%93Shapley_algorithm

CATALOG
    FEATURED TAGS
    rust editor vim emacs editors repost nginx programming neovim tools philosophy ted docker design Go
    FRIENDS